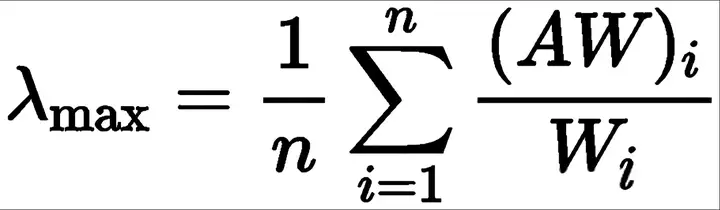AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初提出，适用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题。
AHP层次分析法的优势是将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。
该方法自1982年被介绍到我国以来，以其系统性，简洁实用，所需定量数据信息少等优点，迅速地在社会各个领域内得到广泛应用。如：安全科学、科学环境、科研评价等等。
注意：层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。
一、基本原理
AHP层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
其层次结构模型为：
- 目标层：决策的目的、要解决的问题；
- 准则层：考虑的因素、决策的准则；
- 方案层：决策时的备选方案；
例如现在想选择一个最佳旅游景点，当前有三个选择标准（分别是景色，门票和交通），并且对应有三种选择方案。现通过旅游专家打分，希望结合三个选择标准，选出最佳方案——即最终决定去哪个景区旅游。
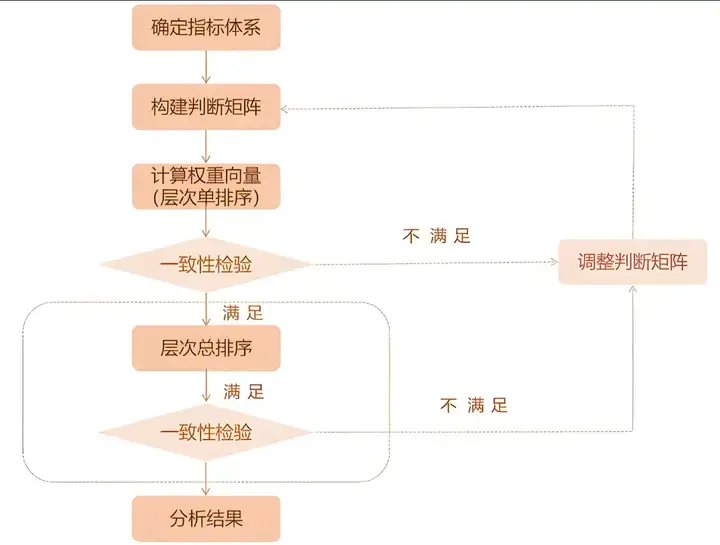
层次分析法的步骤，大体可分为以下四步：
-
1.建立层次结构模型；
-
2.构造判断矩阵(也叫成对比较矩阵)；
-
3.层次单排序及其一致性检验；
-
4.层次总排序及其一致性检验；
二、具体分析过程
1.建立层次结构模型
目标层是指决策的目的、要解决的问题；方案层是指决策时的备选方案； 准则层是指考虑的因素、决策的准则。
假设公司要组织员工出去旅游，希望综合满足大家的要求，因此找到10位旅游专家，对旅游的4个影响因素（分别是景色，门票，交通和拥挤度）进行评价（即专家评价），最终得出四个影响因素的权重，然后结合权重值，对3个备选景点计算得分，选择出最佳旅游方案。
- 目标层：选择最优旅游地；
- 准则层：景色、门票、交通和拥挤度；
- 方案层：武汉，长沙，杭州；
2.构造判断矩阵
在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty等人提出一致矩阵法：
- 不把所有因素放在一起比较，而是两两相互比较；
- 对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。
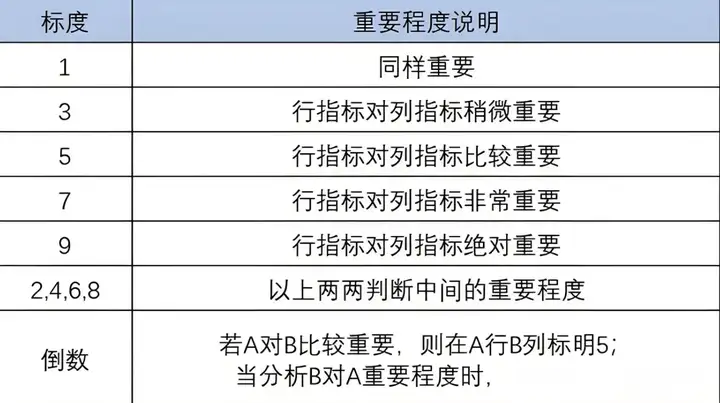
依上例，总共有4个评价因素（即准则层为4项，分别是景色，门票，交通和拥挤度），共有10位旅游专家进行打分，我们采用1-5分标度法，即比如A因素相对B因素非常重要，此时打5分，那么B因素相对于A因素就是1/5即0.2；A因素相对B因素比较重要，此时打3分；A因素相对B因素重要程度一样，此时为1分。
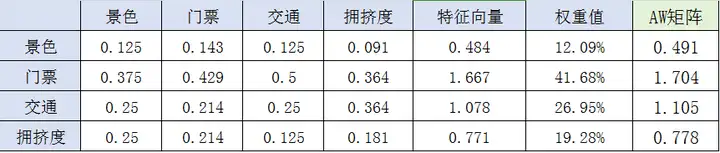
根据10位旅游专家打分，最终将10位旅游的打分进行计算平均分，得到最终的判断矩阵表格，如下：
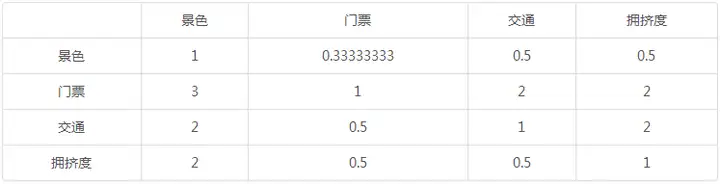
注释：门票相对于景色来讲，重要性更高，所以为3分；相反，景色相对于门票来讲，则为0.33333分。交通相对于景色来更重要为2分，以及拥挤度相对于景色来讲更重要为2分。其余类似下去。
3.层次单排序及其一致性检验
层次单排序是指针对上一层某元素将本层中所有元素两两评比，并开展层次排序， 进行重要顺序的排列，具体计算可依据判断矩阵 A 进行，计算中确保其能够符合 AW= 的特征根和特征向量条件。
简单讲，这一步骤的目的就是计算准则层各因素的权重(特征向量)以及校验上一步骤打分的合理性,不合理则需重新进行打分.
在构建完判断矩阵后，将上述判断矩阵进行归一化处理，即每个单元格纵向归一。
例如：
景色 1/(1+3+2+2) = 0.125
门票 3/(1+3+2+2) = 0.375
...
...第三列
景色 0.5/(0.5+2+1+0.5) = 0.125
门票 2/(0.5+2+1+0.5) = 0.5
...
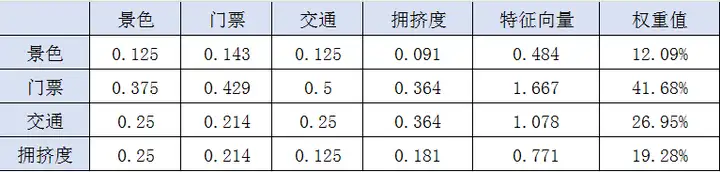
一、权重值
归一化后，再求特征向量和权重值。
特征向量即横向每一行相加。
例如：
景色 0.125+0.143+0.125+0.091 = 0.484
...
交通 0.25+0.214+0.25+0.364 = 1.078
...
权重值即将特征向量再次归一化处理，得出每个特征向量的权重。
例如：
景色 0.484/(0.484+1.667+1.078+0.771) = 12.09%
门票 1.667/(0.484+1.667+1.078+0.771) = 41.68%
...
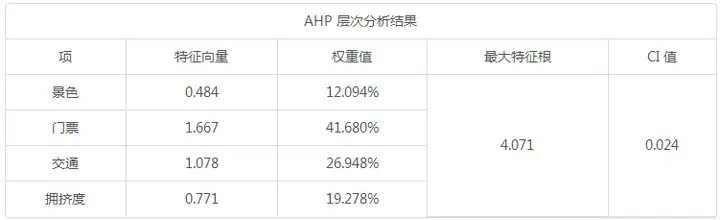
最大特征根的算法：先算出AW矩阵值，再与特征向量权重W相比，最后相加除以n（n为矩阵阶），即得出最大特征根λ。
如：
AW景色 1x12.094%+0.333x41.68%+0.5x26.948%+0.5x19.278% = 0.49083
AW门票 3x12.094%+ 1x41.68%+2x26.948%+2x19.278% = 1.70414
AW交通 2x12.094%+0.5x41.68%+1x26.948%+2x19.278% = 1.10532
AW拥挤度 2x12.094%+0.5x41.68%+0.5x26.948%+1x19.278% = 0.7778
最大特征值λmax =
1/4*（0.49/0.12094+1.704/0.4168+1.105/0.26948+0.778/0.19278）=4.071
CI=(4.071-4)/(4-1)=0.024
二、一致性检验
能否确认层次单排序，则需要进行一致性检验，所谓一致性检验是指对A确定不一致的允许范围。
在构建判断矩阵时，有可能会出现逻辑性错误，比如A比B重要，B比C重要，但却又出现C比A重要。
(当对比因素比较多的时候，难免会出现A>B，B>C，C>A的悖论选择.)
因此在构建完矩阵后,需要使用一致性检验矩阵是否有问题.一致性指标用CI计算，CI越小，说明一致性越大：
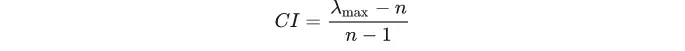
注意：CI=0，有完全的一致性；CI 接近于0，有满意的一致性；CI 越大，不一致越严重。
例如：CI = (4.071-4)/(4-1) = 0.024
考虑到一致性的偏离可能是由于随机原因造成的,因此引入随机一致性指标RI衡量随机因素所造成的一致性偏离的大小.
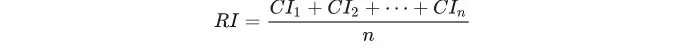
随机一致性指标RI和判断矩阵的阶数有关，一般情况下，矩阵阶数越大，则出现一致性随机偏离的可能性也越大，RI指标通过查表获得.
一致性检验使用CR值进行分析，CR值小于0.1则说明通过一致性检验，反之则说明没有通过一致性检验。如果数据没有通过一致性检验，此时需要检查是否存在逻辑问题等，重新录入判断矩阵进行分析。
针对CR的计算上，CR=CI/RI，CI值在求特征向量时已经得到，RI值则直接查表得出。
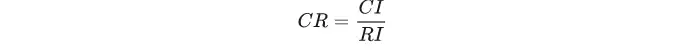
一般，如果CR<0.1 ，则认为该判断矩阵通过一致性检验，否则就不具有满意一致性。
上例矩阵为4阶，因此RI值为0.89.
根据计算，CR=0.024/0.89，最终CR值为0.027，说明通过一致性检验，计算出的权重具有科学性。
至此，我们得出景色、门票、交通和拥挤度对应的权重分别是：12.094%,41.680%,26.948%,19.278%。
4.层次总排序及其一致性检验
上面，我们只是计算了单层排序而得出景色、门票、交通和拥挤度的权重，现在我们要计算某一层次所有因素对于目标层相对重要性的权值。
简单讲，这一步就是通过准则层次单排序的方法来给方案打分。
我们通过层次单排序两两对比各个方案在景色的比较，就可以得到武汉、长沙和杭州的权重，这个权重可作为武汉、长沙和杭州在景色上的得分。
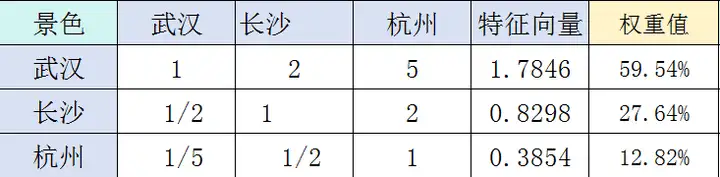
武汉、长沙和杭州在景色上的得分依次是：0.5954、0.2764.0.1282
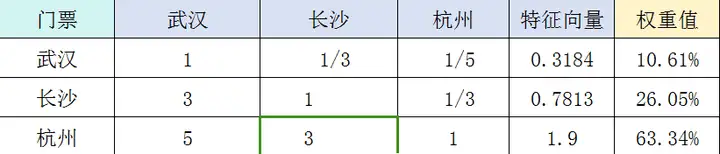
武汉、长沙和杭州在门票上的得分依次是：0.1061、0.2605、0.6334
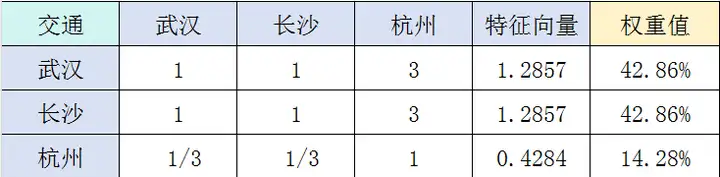
武汉、长沙和杭州在交通上的得分依次是：0.4286、0.4286、0.1428
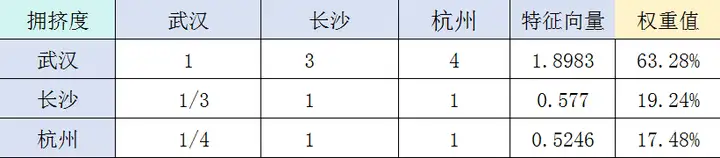
武汉、长沙和杭州在拥挤度上的得分依次是：0.6328、0.1924、0.1748
现在汇总分析，计算各个方案总得分：
武汉：
0.5954x0.12094+0.1061x0.4168+0.4286x0.26948+0.6328x0.19278=0.3537
长沙：
0.2764x0.12094+0.2605x0.4168+0.4286x0.26948+0.1924x0.19278=0.2946
杭州：
0.1282x0.12094+0.6334x0.4168+0.1428x0.26948+0.1748x0.19278=0.3516
武汉>杭州>长沙(0.3537>0.3516>0.2946)
因此，目标层首选旅游地是武汉，次选是杭州。
层次分析法的优点
**系统性：**将对象视作系统，按照分解、比较、判断、综合的思维方式进行决策。成为继机理分析、统计分析之后发展起来的系统分析的重要工具；
**实用性：**一定性与定量相结合，能处理许多用传统的最优化技术无法着手的实际问题，应用范围很广，同时，这种方法使得决策者与决策分析者能够相互沟通，决策者甚至可以直接应用它，这就增加了决策的有效性；
**简洁性：**计算简便，结果明确，具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤，容易被决策者了解和掌握。便于决策者直接了解和掌握。
层次分析法的缺点
**囿旧：**只能从原有的方案中优选一个出来，没有办法得出更好的新方案；
**粗略：**该法中的比较、判断以及结果的计算过程都是粗糙的，不适用于精度较高的问题；
**主观：**从建立层次结构模型到给出判断矩阵，人主观因素对整个过程的影响很大，这就使得结果难以让所有的决策者接受。当然采取专家群体判断的办法是克服这个缺点的一种途径。每一层因素的权重是主观给出，在某些场合会影响泛化性。
三、案例实操
案例1
某位女生A，由于忙于工作，平时没有什么社交，导致一直没找到合适的对象，最后只得走上相亲这条绝路。A找对象的标准，有颜值，身高，存款，性格，以及原生家庭，相亲了3名男生，我们称为张三，李四，王二。现在我们可以建立一个层次结构模型，通过AHP层次分析帮助A找出最优对象。
1.建立层次结构模型
- 目标层：选择最优相亲对象；
- 准则层：颜值、身高、存款、性格和家庭；
- 方案层：张三、李四、王二；
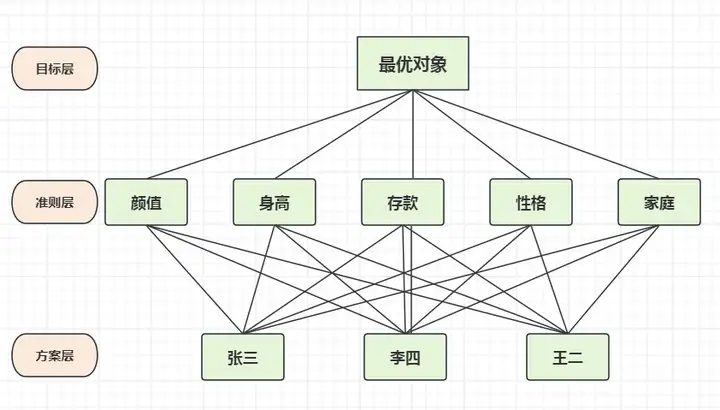
2.构造判断矩阵
通过随机统计一些相亲群体的偏好,来制出这个判断矩阵如下:
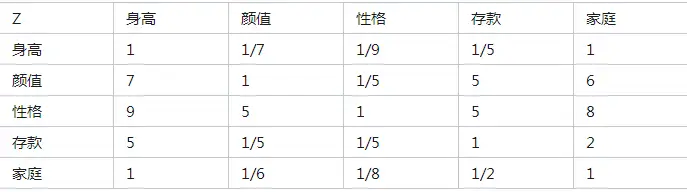
对每一列数据进行归一化,这里我采用的是sum归一化的方式,结果如下:
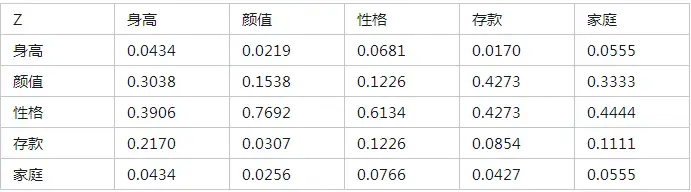
3.层次单排序及其一致性检验
分析结果：
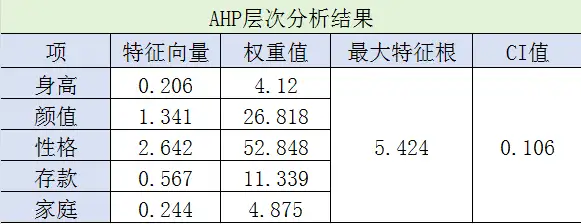
根据RI值表，查看RI值：
计算CR=CI/RI，CR<0.1，说明通过了一致性。
至此，我们得到身高、颜值、性格、存款和家庭对应的权重：0.0412、0.26818、0.52848、0.11339、0.04875。
4.层次总排序及其一致性检验
我们的评判矩阵已经通过一致性检验，现在我们需要对张三、李四和王二进行分析。
张三：身高180，颜值5分，存款30w，性格较差，家庭小康
李四：身高175，颜值8分，存款10w，性格一般，家庭中产
王二：身高170，颜值9分，存款40w，性格较好，家庭富裕
我们分别根据身高、颜值、存款、性格和家庭建立对张三、李四、王二的评判矩阵B1、B2、B3、B4和B5.
重复上面方法，对5个矩阵的每一列归一化，计算出最大特征向量，求CI、RI、CR值，并判断它们的一致性。
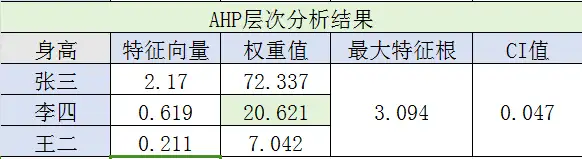
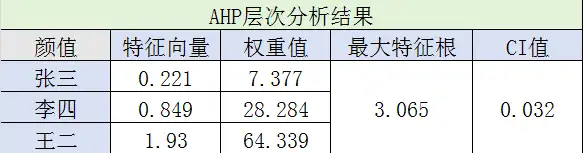
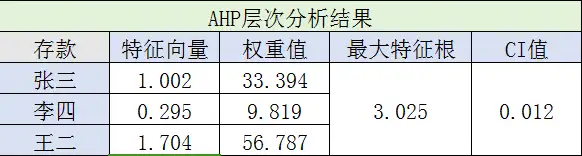
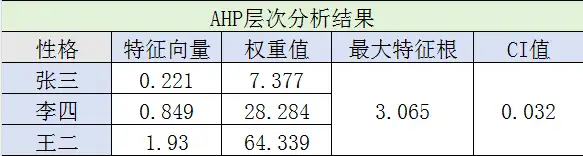
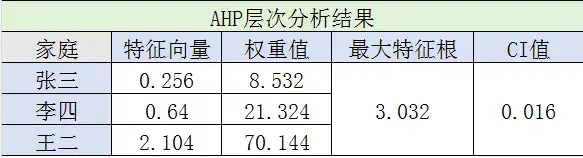
这5个矩阵都通过了一致性检验，在此就没一一列出来了，感兴趣的可以自己去上面查表。
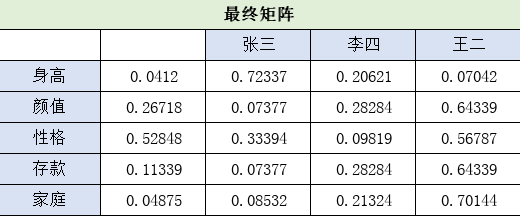
最后，汇总分析：
张三: （0.206x2.17+1.341x0.221+2.642x1.002+0.567x0.221+0.244x0.256）=3.578
李四：（0.206x0.619+1.341x0.849+2.642x0.295+0.567x0.849+0.244x0.64）=2.682
王二: （0.206x0.211+1.341x1.93+2.642x1.704+0.567x1.93+0.244x2.104）=8.741
很明显，王二得分最高，最优质相亲对象还得选王二麻子，虽然身高有点不足，但谁让别人有钱，长得又帅，还会哄人呢！